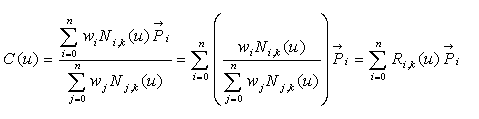
Geometric Modeler

What You Will Learn With This Use Case

The use case explains how to use the CATKnotVector class and the CATNurbsCurve interface to create NURBS curves. The way to use NURBS surface is similar.

[Top]

The Principle

The NURBS (Non Uniform Rational B-Spline) model defines a curve as a piecewise rational polynomial function of a parameter u.

A NURBS curve is defined by control points Pi, i=0..n, whose influence is weighted by rational polynomial functions Ri, i=0..n (dependent on the parameter) and weights wi, i=0..n (independent on the parameter). The rational polynomial functions Ri are defined by the means of a basis, called B-Spline basis, set of piecewise polynomial functions Nik, i=0..n, of same degree k. The degree of the NURBS curve is the degree of the polynomial functions.

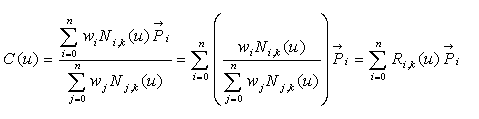
The definition of the basis Nik is uniquely determined by a knot vector, containing the parameters of the limits of pieces of the basis polynomial functions, called arcs. They represent an interval for the parameter values to calculate a segment of shape. The first and last knots correspond to the first and last control point.

In CGM, the CATKnotVector class is used to define the polynomial basis (uniform, periodic, number of arcs, degree) and the CATNurbsCurve is used for the curve definition.

As any CGM curve [3], a CATNurbsCurve is created by the CATGeoFactory, using a knot vector, control points and weights. To remove it, use the CATICGMContainer::Remove method, that removes the instance from the memory, except if it is pointed to by another CGM object (such as a CATPCurve or a CATFace). See [2] to have more detail on the management of the geometric objects.

In case of NURBS surface, two knot vectors must be defined, one in each surface direction.

[Top]

The CAAGobNurbs Use Case

CAAGobNurbs is a use case of the CAAGeometricObjects.edu framework that illustrates GeometricObjects framework capabilities.

[Top]

What Does CAAGobNurbs Do

With this use case, you create a Bézier arc, a Non Uniform Polynomial B-Spline and a Non Uniform Rational B-Spline. Geometric points corresponding to the arc limits are also created.

[Top]

How to Launch CAAGobNurbs

To launch CAAGobNurbs, you will need to set up the build time environment, then compile CAAGobNurbs.m along with its prerequisites, set up the run time environment, and then execute the use case [4].

If you simply type CAAGobNurbs with no argument, the use case executes, but doesn't save the result in an NCGM file. If you want to save this result, provide the full pathname of the NCGM file to create. For example:

With Windows CAAGobNurbs e:\NurbsCreation.NCGM

With UNIX CAAGobNurbs /u/NurbsCreation.NCGM

This NCGM file can be displayed using the CAAGemBrowser use case.

[Top]

Where to Find the CAAGobNurbs Code

The CAAGobNurbs use case is made of a main named CAAGobNurbs.cpp located in the CAAGobNurbs.m module of the CAAGeometricObjects.edu framework:

where InstallRootDirectory is the directory where the CAA CD-ROM is installed.

[Top]

Step-by-Step

The main program is divided into the following steps:

1. Creating the Geometry Factory
2. Creating a Bézier Curve; also creating the geometric points corresponding to the control points to visualize them
3. Creating Another Curve, Only Differing by a Control Point
4. Creating a Non Uniform Polynomial B-Spline
5. Creating the Geometric Points Corresponding to the Arc Limits
6. Creating a General NURBS Curve
7. Writing the Model And Closing the Container

[Top]

Creating the Geometry Factory

The geometry factory (CATGeoFactory) creates and manages all the CATICGMObject (and the curves and surfaces in particular) [3]. This creation is done by the global function ::CATCreateCGMContainer. Notice that the factory can be defined by reading a NCGM file that was previously stored. In that case, the global function ::CATLoadCGMContainer must be used.

CATGeoFactory* piGeomFactory = ::CATCreateCGMContainer() ;
if (NULL==piGeomFactory) return (1);

[Top]

Creating a Bézier Curve

The Bézier curve is a special type of NURBS curve: the multiplicities of the knots is equal to the degree.

The default constructor of CATKnotVector defines a basis for a Bézier curve of degree 3 with one arc. To create a curve using this knot vector, one must define four control points, according to the relation between the continuity (k), the number of arcs (l), and the number of control points (n+1):

l = n - k

 // by default, the constructor builds an appropriate knot vector 
 //             for a Bézier curve
 CATKnotVector bezierKnot;
 // only polynomial
 long isRational=0;
 // hence, no weight
 double * aWeights=NULL;
 // the four control points
 CATMathSetOfPoints vertices(4);
 vertices.SetPoint(CATMathPoint(-20.,0.,0.),0);
 vertices.SetPoint(CATMathPoint(-20.,5.,0.),1);
 vertices.SetPoint(CATMathPoint(-10.,5.,0.),2);
 vertices.SetPoint(CATMathPoint(-10.,0.,0.),3);

 // Creates the NURBS	
 CATNurbsCurve * piFirstCurve = piGeomFactory->CreateNurbsCurve(
                              bezierKnot,
                              isRational,
                              vertices,
                              aWeights);   // NULL (polynomial)
 if (NULL==piFirstCurve)
 {
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
 }
	
 // Creates the geometric points to visualize the control points
 CATCartesianPoint* piCP1= piGeomFactory->CreateCartesianPoint
                                             (CATMathPoint(-20.,0.,0.));
 CATCartesianPoint* piCP2= piGeomFactory->CreateCartesianPoint
                                             (CATMathPoint(-20.,5.,0.));
 CATCartesianPoint* piCP3= piGeomFactory->CreateCartesianPoint
                                             (CATMathPoint(-10.,5.,0.));
 CATCartesianPoint* piCP4= piGeomFactory->CreateCartesianPoint
                                             (CATMathPoint(-10.,0.,0.));
 if (NULL==piCP1 || NULL==piCP2 || NULL==piCP3 || NULL==piCP4)
 {
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
 }

The control points of the curves are given as mathematical points to the CreateNurbsCurve method of CATGeoFactory that creates the object (Fig. 1 displays the result).

To visualize the control points, the use case creates them as geometric points, but this is not required in the general use.

If an error occurs, the program closes the factory and returns an error code.

[Top]

Creating Another Curve, Only Differing by a Control Point

To see the influence of the control points, another Bézier curve using the same knot vector is created: only one control point is different.

Fig. 1: Illustration of the Steps 2 And 3

The green curve has four control points (CP1 to CP4). If you move CP3 to CP3', the curve is attracted by this new points. Notice two important properties of this kind of NURBS, called Bezier curve: The curve is inside the convex hull of the control points The curve is tangent to the segment joining the first and second control points at the beginning of the curve, and to the segment joining the last and next to last control points at its end.

To change the control point, directly change the definition in the CATMathSetOfPoint: the position of the point in the CATMathSetOfPoint is an index (beginning at 0).

 vertices.SetPoint(CATMathPoint(-5,15,0),2);
 CATNurbsCurve * piSecondCurve = piGeomFactory->CreateNurbsCurve(
                         bezierKnot,
                         isRational,
                         vertices,
                         aWeights);     // NULL (polynomial)
 if (NULL==piSecondCurve)
 {
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
 }

 CATCartesianPoint* piCP3bis= piGeomFactory->CreateCartesianPoint
                                             (CATMathPoint(-5.,15.,0.));
 if (NULL==piCP3bis)
 {
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
 }	

[Top]

Creating a Non Uniform Polynomial B-Spline

We define here the green curve of Fig. 2. It is non periodic, non uniform, and C2 continuous, with three arcs of degree 3 (the knot vector has four distincts knots). In this case, there are six control points, according to the following relation [1] between the number of knots (m+1), the degree (k) of Nik and the number of control points (n+1):

m = (n+1) + k

 const long nbknots=4;
 double aKnots[nbknots];
 aKnots[0]=0;
 aKnots[1]=2;
 aKnots[2]=8;
 aKnots[3]=9;
 long isPeriodic=0;   // non periodic
 long continuity=2;   // C2 continuity
 CATKnotVector nonUniformKnot(isPeriodic,nbknots,aKnots,continuity);
	
 // the six control points
 CATMathSetOfPoints otherVertices(6);
 otherVertices.SetPoint(CATMathPoint( 20., 0.,0.),0);
 otherVertices.SetPoint(CATMathPoint( 22.,10.,0.),1);
 otherVertices.SetPoint(CATMathPoint( 30.,20.,0.),2);
 otherVertices.SetPoint(CATMathPoint( 40., 0.,0.),3);
 otherVertices.SetPoint(CATMathPoint( 43.,15.,0.),4);
 otherVertices.SetPoint(CATMathPoint( 50.,20.,0.),5);
	
	
 CATNurbsCurve * piThirdCurve = piGeomFactory->CreateNurbsCurve(
                                   nonUniformKnot,
                                   isRational,
                                   otherVertices,
                                   aWeights);          // NULL (polynomial)
 if (NULL==piThirdCurve)
 {
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
 }

The knot vector is now non uniform, because its knot values do not increment of 1. The curve is still polynomial, because the pointer to the weight values is NULL. In fact, the weight of each control point is 1..

[Top]

Creating the Geometric Points Corresponding to the Arc Limits

The arc limits are defined by the knots. By default, the CreateNurbsCurve method adapts the parameterization of the knots according, more or less, to the length of the curve.

Hence, if you asked for the knot vector of ThirdCurve (GetKnotVector), that was created at the step 4, you find new knots values. If you want the curve to keep its initial parameterization, use the CatKeepParameterization value of the CATParameterizationOption (optional argument). Remember that the first and last knots correspond to the first and last control point, and that the knots are the arc limits.

CATCrvParam param;
CATCrvEvalLocal result;
CATMathPoint mathPoint;
// new CATKnotVector 
const CATKnotVector * pNewKnotVector=piThirdCurve->GetKnotVector();
if (NULL==pNewKnotVector)
{
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
}
const double * aNewKnots=NULL;
pNewKnotVector->GetKnots(aNewKnots);
if (NULL==aNewKnots)
{
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
}

// second knot value 
piThirdCurve->CreateParam(aNewKnots[1] ,param);
piThirdCurve->Eval(param,CATCrvEvalCommand::EvalPoint,result);
	
result.GetPoint(mathPoint);
CATCartesianPoint* piCPAL2= piGeomFactory->CreateCartesianPoint(mathPoint);
if (NULL==piCPAL2 )
{
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
}     

To create the 3D geometric point, you have to recover its definition from the parameter (the knot): this is done by using the curve evaluator:

• The Eval method computes the evaluation: the type of evaluation is given by a CATCrvEvalCommand: here, only the point evaluation
• The GetPoint method returns the result as a mathematical point.

It just remains to create the corresponding point to be able to visualize the arc limits.

[Top]

Creating a General NURBS Curve

The non uniform vector of the step 5 is kept. The non rational is created by defining weights affected to the control points

 isRational=1;
 aWeights=new double[6];
 aWeights[0]=1;
 aWeights[1]=1;
 aWeights[2]=10;
 aWeights[3]=20;
 aWeights[4]=5;
 aWeights[5]=1;
 CATNurbsCurve * piFourthCurve = piGeomFactory->CreateNurbsCurve(
                   nonUniformKnot,
                   isRational,          // Yes
                   otherVertices,
                   aWeights);           // Not NULL
 if (NULL==piFourthCurve)
 {
   ::CATCloseCGMContainer(piGeomFactory);
   return (1);
 } 
	
 delete [] aWeights;
 aWeights = NULL;

Fig. 2 shows the influence of the weights.

Fig. 2: Illustration of Non Uniform Polynomial and Rational B-Splines

The green curve is the non uniform polynomial B-Spline curve created at the step 4. The weight of each control point is 1. If you assign the (1,1,10,20,5,1) weights to the control points, it gives the red curve. This curve is attracted by the control points CP3 and CP4, that are more weighted than the others. These curves have three arcs: CP1-K1, K1-K2, K2-CP2.

[Top]

Writing the Model and Closing the Container

To save the model in a file, the ::CATSaveCGMContainer global function is used. Notice that in the use case, the save is conditioned by an input parameter representing the file inside which the model must be saved.

The use case ends with the closure of the geometry factory, done by the ::CATCloseCGMContainer global function.

 if(1==toStore)
 {
#ifdef _WINDOWS_SOURCE
   ofstream filetowrite(pfileName, ios::binary ) ;
#else
   ofstream filetowrite(pfileName,ios::out,filebuf::openprot) ;
#endif

   ::CATSaveCGMContainer(piGeomFactory,filetowrite);
   filetowrite.close();
 }	

 //
 // Closes the container
 //	
 ::CATCloseCGMContainer(piGeomFactory);

[Top]

In Short

This use case describes how to use the NURBS curves in CGM, using the CATNurbsCurve interface and the CATKnotVector class. Bézier curve, non uniform polynomial curve and non uniform rational curve are then created.

[Top]

References

History

Copyright © 2000, Dassault Systèmes. All rights reserved.