Geometric Modeler

What You Will Learn With This Use Case

This use case is intended to help you create a geometric helix, then transform it into a wire.

[Top]

The CAATopCreateHelix Use Case

CAATopCreateHelix is a use case of the CAATopologicalOperators.edu framework that illustrates how to create a geometric helix and convert it into a wire.

[Top]

What Does CAATopCreateHelix Do?

The CAATopCreateHelix use case:

• creates the geometry factory, CATSoftwareConfiguration and CATTopData
• creates an helix with a constant pitch  and a constant radius and creates the body associated with the helix
• creates an helix with a variable pitch  and a constant radius and creates the body associated with the helix
• writes the model and closes the container.

[Top]

How to Launch CAATopCreateHelix

To launch CAATopCreateHelix, you will need to set up the build time environment, then compile CAATopCreateHelix.m along with its prerequisites, set up the run time environment, and then execute the use case [1].

If you simply type CAATopCreateHelix with no argument, the use case executes, but doesn't save the result in an NCGM file. If you want to save this result, provide the full pathname of the NCGM file to create. For example:

With Windows CAATopCreateHelix e:\helix.NCGM

With UNIX CAATopCreateHelix /u/helix.NCGM

This NCGM file can be displayed using the CAAGemBrowser use case.

[Top]

Where to Find the CAATopCreateHelix Code

The CAATopCreateHelix use case is made of a main named CAATopCreateHelix .cpp located in the CAATopCreateHelix .m module of the CAATopologicalOperators.edu framework:

where InstallRootDirectory is the directory where the CAA CD-ROM is installed.

[Top]

Step-by-Step

Creating the Geometry Factory, CATSoftwareConfiguration and CATTopData

 The geometry factory (CATGeoFactory) creates and manages all the CATICGMObject. This creation is done by the global function ::CATCreateCGMContainer. Notice that the factory can be defined by reading a NCGM file that was previously stored. In that case, the global function ::CATLoadCGMContainer must be used.

CATGeoFactory* piGeomFactory = ::CATCreateCGMContainer() ;
if (NULL==piGeomFactory) return (1);

CATSoftwareConfiguration * pConfig = new CATSoftwareConfiguration();
CATTopData topdata(pConfig);

[Top]

Creating an Helix with a Constant Pitch and Constant Radius

An helix with a constant pitch is created by using the CATGeoFactory::CreateHelix API. With this method, you can specify either a constant radius (last argument set to 0) or a linear variation coefficient for the radius (number of mm per helix turn).

With the code below:

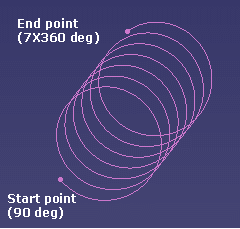
// (a) - Create the CATHelix
CATHelix * pHelix0 = piGeomFactory->CreateHelix(helixAxis, /* the axis oz */
B,                                                          /* the origin */
90*CATDegreeToRadian,                       /* the start angle in radians */
7*CAT2PI,                                     /* the end angle in radians */ 
20,                                                          /* the pitch */ 
1,                            /* the orientation with respect to the axis */
0);                            /* the radius evolution = number of mm/turn*/

you get the helix below:

Note that the origin point (B) does not belong to the helix as the start angle is set to 90 deg. To have the origin confused with the starting point, you should specify a start angle of 0.

[Top]

Creating an Helix with a Variable Pitch and a Variable Radius

To create an helix with a variable pitch and a variable radius (with a linear or not linear variation), you must use the CATHelix::Set API which takes CATLaws as arguments. Prior to calling this method, you must:

1. Initialize the data for the helix to be created. To do this, use the CATGeoFactory::CreateHelix method
2. Compute the length of the initial helix by using the CATDynMassProperties1D operator. A suitable length is required for the CATLaw creation. If you pass an inconsistent length to the CATLaw and CATHelix::Set method, you will get a throw.

Creating the Radius Law

A linear radius law is used as it can be used both for a constant and a linear law.

// (c) - create the radius linear law: radius is 100
CATLaw * radiusLaw = ((CATLaw*)(piGeomFactory -> CreateLinearLaw(0.0, 100.0, theLength1, 100)));

Creating the ZLaw as a CATCompositeLaw

The ZLaw defines how the Z coordinate varies versus the CATCrvParam. A composite law with one CATMathFunctionX of degree 2 is defined (z = 0.02*CATCrvParam ²).

// (d) - create the law which defines how the 
// helix is developed along the helix axis
// at the beginning of the curve, the z coordinate is 0.
// at the end of the curve, the Z coordinate is 0 + 0 + 0.02*(CATCrvParam)**2
const CATMathFunctionX ** Functions1 = new const CATMathFunctionX * [1];
double array1[3] = {0.0,0,0.02}; 
Functions1[0] = new CATMathPolynomX(2,array1); 
CATLaw * ZLaw = (CATLaw*)piGeomFactory->CreateCompositeLaw (1,LimitParameters1,Functions1);

Creating the theta law as a linear law

// (e) - create the linear law for the angle (number of turns = 9)
// at the beginning of the curve, the number of turns is 0
// at the end it is 9.
CATLaw * thetaLaw = ((CATLaw*)(piGeomFactory -> CreateLinearLaw(0.0, 0.0, theLength1, 9*CAT2PI)));

 Setting the New Helix Parameters

The arguments 4 to 6 allow you to modify the helix shape by applying a coefficient to the coordinates. The effect of these parameters is illustrated below.

// The vector which defines the helix axis (Oz)
CATMathVector iUnitZ (0.,0.,1.); 
// The vector to be used as reference for angles and turns (Ox)
CATMathVector iUnitu (1.,0.,0.); 

pHelix1->Set(O, iUnitZ, iUnitu, 
                1, 1, 1,     // no ratio applied to the helix coordinates
                radiusLaw,   // the radius law
                ZLaw,        // the law along z
                thetaLaw,    // the theta law
                90*CATDegreeToRadian,   // the start angle
                1);                     // the orientation

For how to create a skin, see the CAATopOverview use case.

[Top]

The Created Helix

constant radius = 100.0 Z = 0.02*CATCrvParam 2 ThetaLaw = linear [0, 9 * 360deg] CATCrvParam Max = 125.664 -> Z max = 315.827 no ratio applied to coordinates

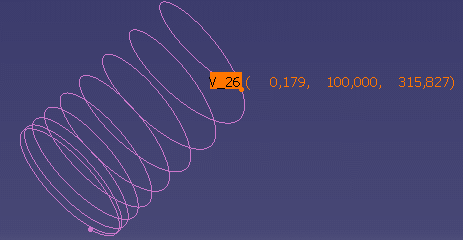What you get if you modify the radius law

linear variation radius = 100.0 - 150.0 Z = 0.02*CATCrvParam 2 ThetaLaw = linear [0, 9 * 360deg] CATCrvParam Max = 125.664 -> Z max = 315.827 no ratio applied to coordinates

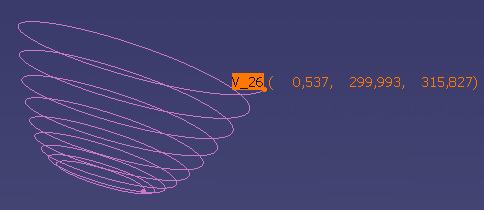[Top]

What you get if you apply a ratio to the x coordinate

linear variation radius = 100.0 - 150.0 Z = 0.02*CATCrvParam 2 ThetaLaw = linear [0, 9 * 360deg] CATCrvParam Max = 125.664 -> Z max = 315.827  pHelix1->Set(O, iUnitZ, iUnitu, 2, 1, 1, //  ratio = 2  applied to the x coordinate

[Top]

Writing the Model and Closing the Factory

To save the model in a file, the ::CATSaveCGMContainer global function is used. Notice that in the use case, the save is conditioned by an input parameter representing the file inside which the model must be saved.

The use case ends with the closure of the geometry factory, done by the ::CATCloseCGMContainer global function.

 if(1==toStore)
 {
#ifdef _WINDOWS_SOURCE
   ofstream filetowrite(pfileName, ios::binary ) ;
#else
   ofstream filetowrite(pfileName,ios::out,filebuf::openprot) ;
#endif

   ::CATSaveCGMContainer(piGeomFactory,filetowrite);
   filetowrite.close();
 }	

 //
 // Closes the container
 //	
 ::CATCloseCGMContainer(piGeomFactory);

[Top]

References

History

Copyright © 2005, Dassault Systèmes. All rights reserved.