Geometric Modeler

What You Will Learn With This Use Case

This use case is intended to help you to use the mathematical classes. It first gives general features on these classes, then proposes examples of use:

• Creation of mathematical points, lines, vectors; use of operators
• Search for the eigen values and vectors of a 3x3 matrix
• Define a transformation of axis systems.

[Top]

General Features of Mathematical Classes

The Mathematics framework provides the basic mathematical classes (such as planes, 2D/3D vectors, 2D/3D points, 2D/3D matrices) and their associated usual behavior: for example, the norm of a vector, the determinant, the trace or the inverse of a matrix.

These mathematical classes are concrete (as opposed to the interfaces), and are optimized to give the best performance. Their instances cannot be streamed. In fact, they are not dedicated to be stored but only to be used in a transient way.

The mathematical classes use the operators (+, *, ^), when this makes sense: hence, you can add two vectors with the + operator, or define a vector by subtracting a point to another one.

The methods of the mathematical classes always consider that their outputs are allocated by the caller: in that way, the caller completely manages the memory, and can optimize its use. Now, following the CAA naming conventions of the arguments, all their arguments must be named with the i prefix, even the outputs (resource allocated and deallocated by the caller). This is not very significant for distinguishing which is really modified. Hence, the "output" arguments are denoted with an io prefix.

[Top]

The CAAMthBase Use Case

CAAMthBase is a use case of the CAAMathematics.edu framework that illustrates Mathematics framework capabilities.

[Top]

What Does CAAMthBase Do

Fig. 1: The Objects Used In the CAAMthBase Use Case

In this use case, you use the CATMathPoint, CATMathVector, CATMathLine, CATMathAxis and CATMathTransformation classes.

[Top]

How to Launch CAAMthBase

To launch CAAMthBase, you will need to set up the build time environment, then compile CAAMthBase.m along with its prerequisites, set up the run time environment, and then execute the use case [1].

[Top]

Where to Find the CAAMthBase Code

The CAAMthBase use case is made of a main named CAAMthBase.cpp located in the CAAMthBase.m module of the CAAMathematics.edu framework:

where InstallRootDirectory is the directory where the CAA CD-ROM is installed.

[Top]

Step-by-Step

There are three logical sections in CAAMthBase:

1. Creating Instances Points, Vectors, Lines directly or by the means of operators
2. Searching For the Eigen Values and Vectors Of a 3x3 Matrix
3. Defining a Transformation of Axis Systems

We now comment each of those sections by looking at the code.

[Top]

Creating Points, Vectors, Lines

CATMathPoint 	O, A(20. ,10. ,0.) ; // Default constructor, O is (0.,0.,0.)
	
CATMathVector u(10., 20. ,0.);
u.Normalize();                     // Normalize u;
	
// H: Orthogonal projection of A on the line (O,u): 
// Use the operators 
// A-O is a vector, (A-O)*u the dot product
//
CATMathVector OA = A - O ;
CATMathPoint  H  = O + ( OA*u ) * u;
 
// Computes the normal of the two vectors (A-O) and u: ^ is the cross product
CATMathVector n  = OA ^ u;      
	
//
// Another way to project to get H: 
// use the Project method of the CATMathLine class. 
//
CATMathLine  line(O,u);
CATMathPoint projection;
line.Project( A , projection );
	 
// Returns the distance between the two computed points. 
//If non nul, it is an error.
		
if ( H.SquareDistanceTo( projection ) != 0.  ) return (1);
	
// Outputs the coordinates of the projected points
double aCoord[3];
H.GetCoord( aCoord );
cout << "coordinates of the projected point : " 
		<< aCoord[0] << "\t" 
		<< aCoord[1] << "\t"
		<< aCoord[2] << endl;

Notice:

• The use of the operators: A-O is a vector, (A-O)*u the dot product, ^ is the cross product.
• The allocation of the memory by the caller; the aCoord array for example.

[Top]

Searching For the Eigen Values and Vectors of a 3x3 Matrix

// M=  0. 12.  13.
//    21.  0.  23.
//    31.  32.  0. 
	
CATMath3x3Matrix M ( 0.,  0.,  0., 
		    21.,  0.,  0.,
	            31., 32.,  0.);
	
// It is not invertible
CATMath3x3Matrix N;
if ( M.Inverse( N ) ) return (2);
	
// Retrieves the eigen vectors and values
int	      nbValues;
double	      aEigenValues [3];
CATBoolean    aHasAssociatedVector[3];
CATMathVector aEigenVectors[3];
CATBoolean    isDiagonal;
	
M.EigenVectors( nbValues , 
		aEigenValues , 
		aHasAssociatedVector , 
		aEigenVectors , 
		isDiagonal );

for(int i = 0 ; i < nbValues ; i++ )
{
	cout << "Eigen value number " << i+1 << " : " << aEigenValues[i];
	if (aHasAssociatedVector[i]) 
	{
	   cout << " eigen vector "	<< aEigenVectors[i].GetX() << "\t"
		<< aEigenVectors[i].GetY() << "\t"
		<< aEigenVectors[i].GetZ() << endl;
	}
	else
	{
	   cout << " no associated eigen vector " << endl;
	}
		
}

The method to search the eigen values and vectors takes into account the case where there is no vector associated with an eigen value, that is to say when the dimension of the associated eigenspace is less than the multiplicity of the eigenvalue. Hence, the aHasAssociated array allows the caller to test whether this vector exists.

Notice also that all the arrays are allocated by the caller.

[Top]

Defining a transformation of axis systems

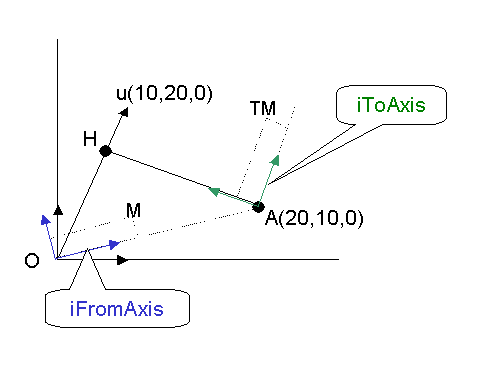
To define the tranformation of an axis system into another one, one has to combine two transformations:

• the first from the final axes system to the canonical
• the second from the canonical axes system to the initial.

The constructor of CATMathAxis takes a point and three vectors as input arguments. If these arguments are omitted, default values are used.

The constructor uses the three input vectors as follows:

• U is normalized (if needed) to become the axis first direction.
• The axis second direction belongs to the plane (U, V) and is orthogonal to U.
• W is used to give the orientation of the axis system.

Although the input vectors can be not normalized and orthogonal, there resulting axis has three normalized and orthogonal directions.

CATMathAxis fromAxis ( O , OA , u );    
CATMathAxis toAxis   ( A , u , H-A);
CATMathTransformation transfo2;

// the transformation is defined as the composition 
//of two transformation as follows:
transfo2 = CATMathTransformation ( toAxis,CATMathOIJK ) 
	 * CATMathTransformation ( CATMathOIJK, fromAxis);

// apply it on a point:
CATMathPoint transfoOfO = transfo2 * O;

// the first coordinate of O in fromAxis is negative in toAxis.
if ( transfo2OfO.GetX()>0) return (4) ; 

// the second coordinate of O in fromAxis is positive in toAxis.
 if ( transfo2OfO.GetY()<0) return (4) ; 

• fromAxis is the axes system defined as follows:
  • The point O is the origin,
  • The vector OA is normalized to become the first direction ,
  • The second direction is orthogonal to OA, and in the (OA,u) plane.
  • The third argument is taken by default to the third direction of the canonical axes system. fromAxis third direction is orthogonal to the two firsts, in the orientation defined by the third argument
• CATMathOIJK represents the canonical axis system.
• Notice the use of the * operator.

[Top]

In Short

This article has proposed milestones to use the mathematical classes, and has illustrated them on some examples.

[Top]

References

History

Copyright © 2000, Dassault Systèmes. All rights reserved.