Foreign Mathematical Functions

Geometric Modeler	Mathematics	Foreign Mathematical Functions The mathematical definition of the external geometric surfaces
Use Case

Abstract

The AdvancedMathematics framework mainly exposes the mathematical functions and sets of mathematical points. The mathematical functions are used as evaluators by the geometric objects. If you want to introduce your own geometric object with associated mathematical equations that are not provided by the AdvancedMathematics framework, you can derive your own mathematical function. This article discusses how to introduce your own function class. The new class is used to demonstrate how to evaluate the mathematical functions.

What You Will Learn With This Use Case
The Principle
The CAAAmtForeign Use Case
Step-by-Step
In Short
References

What You Will Learn With This Use Case

This use case explains the introduction of a new class of mathematical function by describing all the steps of its introduction on a concrete case: the new function to introduce is a function of two parameters (called u and v) to R, and defined by:

(u,v) -> F(u,v) = a*u + b*v + c * cos(u)*cos(v) + d

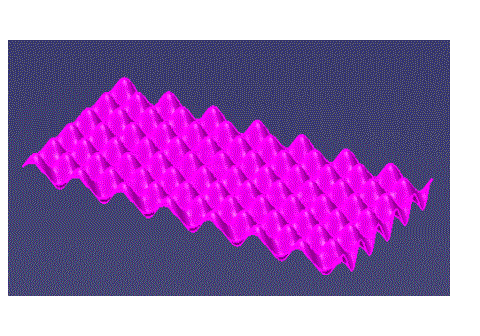
where a, b, c, d are definition parameters. This function can be later used to defined the evaluators of a surface called "eggs box".

*Fig 1*: The "Eggs Box" using the new type of function
	The surface is defined by three functions, one for each Cartesian coordinate: FX(u,v) = a_xu + b_xv + d_x FY(u,v) = a_yu + b_yv + d_y FZ(u,v) = c_z cos(u)cos(v) + d_z

[Top]

The Principle

To introduce a new class of mathematical functions, you must derive the base class of the mathematical functions:

CATMathFunctionX for a function of one variable to R
CATMathFunctionXY for a function of two variables to R

and override the corresponding methods.

The mandatory methods to provide are:

IsA(): returns the class name of the new class
Eval(): evaluates the function.

In this case, the higher order evaluators are approximated. However, it is strongly recommended

To override the first derivative evaluations: EvalFirstDerivX, EvalFirstDerivY
The best being to also write the second derivative evaluations: EvalSecondDerivX2, EvalSecondDerivXY, EvalSecondDerivY2.

In these cases, the IsOption method must also be overridden: it defines what kind of evaluators are available.

Finally, third derivatives can be provided, as well as multiple evaluations.

[Top]

The CAAAmtForeign Use Case

CAAAmtForeign is a use case of the CAAAdvancedMathematics.edu framework that illustrates AdvancedMathematics framework capabilities.

[Top]

What Does CAAAmtForeign Do

This use case:

First derives the new class, and provides the corresponding overridden methods
Then uses the new class to evaluate the function. In this part, what is done for the foreign function is exactly the same as what must be done for any mathematical function: the use is the same.

[Top]

How to Launch CAAAmtForeign

To launch CAAAmtForeign, you will need to set up the build time environment, compile CAAAmtForeignFct.m and CAAAmtFct.m along with their prerequisites, set up the run time environment, and then execute the use case by launching the executable CAAAmtFct.exe as described in [1]. The use case writes on the standard output the following line:

13.6762, 13.6762

Remember that this use case only uses mathematical objects, so that nothing can be streamed. Fig.1 is a representation of the use of these mathematical functions to create new classes of geometric objects, as presented in the CAAGobForeign use case.

[Top]

Where to Find the CAAAmtForeign Code

The CAAAmtForeign use case is made of

The header CAAAmtForeignFctXY.h of the new class located in the ProtectedInterfaces directory of the CAAAdvancedMathematics.edu framework
The corresponding source code CAAAmtForeignFctXY.cpp located in the CAAAmtForeignFct.m module of the CAAAdvancedMathematics.edu framework
A main named CAAAmtFctMain.cpp located in the CAAAmtFct.m module of the CAAAdvancedMathematics.edu framework, using the new class.

Windows	`InstallRootDirectory\CAAAdvancedMathematics.edu\CAAAmtFct.m\`
Unix	`InstallRootDirectory/CAAAdvancedMathematics.edu/CAAAmtFct.m/`

where InstallRootDirectory is the directory where the CAA CD-ROM is installed.

This architecture allows us to export the definition of the new class: hence, it can be used in other frameworks, and especially in the GeometricObjects framework to create a new class of surface.

[Top]

Step-by-Step

We first look at the header of the foreign function class: there is a constructor and the mandatory methods are overridden. Moreover, we choose to override the evaluators of the first and second derivatives, as well as the multiple evaluators: in this use case, this will allow us to have better performance, see the code.

CAAAmtForeign is made of the following steps:

The CAAAmtForeignFctXY.h Header
The CAAAmtForeignFctXY.cpp Source Code
The CAAAmtFctMain.cpp Main: How to Evaluate a Mathematical Function

[Top]

The CAAAmtForeignFctXY. Header h

class ExportedByCAAAmtForeignFct CAAAmtForeignFctXY : public CATMathFunctionXY
{
 public:
  //-----------------------------------------------------------------
  // Constructors
  //-----------------------------------------------------------------
  CAAAmtForeignFctXY(const double iA,
                     const double iB,
                     const double iC,
                     const double iOrigin);
                                      
  //-----------------------------------------------------------------
  // Information methods
  //-----------------------------------------------------------------
  //Returns "CAAAmtForeignFctXY"
  CATMathClassId IsA() const; 
  // the type of available evaluations
  CATBoolean IsOption(const CATMathOption iOption) const;  
   
  //-----------------------------------------------------------------
  // Evaluators on doubles
  //-----------------------------------------------------------------
   double Eval(const double & iX, const double & iY) const;

  // first derivatives 
  double EvalFirstDerivX(const double & iX, const double & iY) const;
  double EvalFirstDerivY(const double & iX, const double & iY) const;
  // ... other overridden methods

  // multiple evaluations
  void Eval(const double u, 
            const double v, 
	    const CATMathOption iOptions,
	    double * ioF,
	    double * ioFx =NULL, 
            double * ioFy =NULL,
	    double * ioFx2=NULL, 
            double * ioFxy=NULL, 
            double * ioFy2=NULL) const;
  // ... other overriden methods
private:
  double _a, _b, _c, _Origin;
};

#endif

The ExportedByCAAAmtForeign variable is defined in the CAAAmtForeignFct.h header. CAAAmtForeignFunctionXY is a scalar function of two variables (named here iX and iY). When used to define the mathematical definition of a surface, this two variables are often called iU and iV.

[Top]

The CAAAmtForeignFctXY.cpp Code

This section emphasizes on some methods of the .cpp. The IsOption method describes the type of evaluators that are overridden by the foreign surface.

CATBoolean CAAAmtForeignFctXY::IsOption(const CATMathOption iOption) const
{
  CATMathOption myOptions = 
    OptionEval + OptionEvalFirstDeriv + OptionEvalSecondDeriv ;

   if ((myOptions & iOption) == iOption) return (1);   
   return (0); 
}

It is important that the declaration of the IsOption method and the actual redefined methods are consistent. If not, some problems could appear during the use of the new function. Now follows the code of the function evaluator and the first derivative evaluator.

//-----------------------------------------------------------------
// CAAAmtForeignFctXY::Evaluators on doubles
//-----------------------------------------------------------------
double CAAAmtForeignFctXY::Eval(const double & u, 
                                const double & v) const
{
  return (_a*u+_b*v+_c*cos(u)*cos(v)+_Origin);
}

double CAAAmtForeignFctXY::EvalFirstDerivX(const double & u, 
                                           const double & v) const
{
  return (_a-_c*sin(u)*cos(v));
}

double CAAAmtForeignFctXY::EvalFirstDerivY(const double & u, 
                                           const double & v) const
{
  return (_b-_c*cos(u)*sin(v));
}

In the case of the CAAAmtForeignFctXY, it is interesting to override the multi evaluator method: the cosine and sine values are once computed and stored in an array, instead of being computed again at each time they are needed. This implementation saves CPU time.

The following code is only an illustration of the fact that, in the case of this particular mathematical definition, some computations can be bufferized.

Overridden the derivatives evaluators is not necessary, because there always is a default implementation of the derivative evaluators and multi-evaluators.

// Multi-evaluation of function and derivatives on a regular 
// grid of Nu x Nv points delimited by  [uStart,uEnd] x [vStart,vEnd]
// The value f[Nv*i+j] contains Eval(x_i,y_j) ...
void CAAAmtForeignFctXY::Eval(const CATMathIntervalND & iDomain, 
                              const long * NbPoints,
                              const CATMathOption iOptions,
                              double * f,
                              double * fx , 
		              double * fy,
                              double * fx2, 
                              double * fxy, 
		              double * fy2) const
{
  // To speed up this multi-evaluation, use a precomputation which computes
  // fast cosinus and sinus evaluations on a regular grid thanks to the formula:
  //    cos(u+delta) = cos(u)*cos(delta)-sin(u)*sin(delta)
  //    sin(u+delta) = cos(u)*sin(delta)-sin(u)*cos(delta)
  long nu = NbPoints[0], nv = NbPoints[1];
  const double * coords = iDomain.GetCoords();
  double uStart = coords[0], uDelta=0.;
  if (nu>1) 
    uDelta = (coords[1]-coords[0])/double(nu-1);
  double vStart = coords[2], vDelta=0.;
  if (nv>1)
    vDelta = (coords[3]-coords[2])/double(nv-1);
  
  // Compute cos(vStart+j*vDelta) and sin(vStart+j*vDelta) and bufferizes them 
  // in sintab and costab arrays to save CPU time in the computation 
  double * costab = new double[2*nv];
  double * sintab = costab + nv;

  double dcos = cos(vDelta), dsin = sin(vDelta);
  costab[0] = cos(vStart);
  sintab[0] = sin(vStart);

  for (long j=1; j<nv; j++) 
	{
    costab[j] = costab[j-1]*dcos-sintab[j-1]*dsin;
    sintab[j] = costab[j-1]*dsin+sintab[j-1]*dcos;
  }

  // Main double loop
  double cosu = cos(uStart);
  double sinu = sin(uStart);
  dcos = cos(uDelta);
  dsin = sin(uDelta);
  double u = uStart;
  for (long i=0; i<nu; i++) {
    if (i>0) {
      double tmp = cosu;
      cosu = cosu*dcos-sinu*dsin;   // c = cos(uStart+i*uDelta)
      sinu = tmp*dsin+sinu*dcos; // s = sin(uStart+i*uDelta)
    }
    double v = vStart;
    for (long j=0; j<nv; j++) {
      if (iOptions & OptionEval)
        *(f++) = _a*u+_b*v+_c*cosu*costab[j]+_Origin;
      if (iOptions & OptionEvalFirstDeriv) 
			{
        *(fx++) = _a-_c*sinu*costab[j];
        *(fy++) = _b-_c*cosu*sintab[j];
      }
      if (iOptions & OptionEvalSecondDeriv) 
			{
        *(fx2++) = *(fy2++) = -_c*cosu*costab[j];
        *(fxy++) = _c*sinu*sintab[j];
      }
      v += vDelta;
    }
    u += uDelta;
  }
  delete [] costab;
}

[Top]

The CAAAmtFctMain.cpp main

The main first creates a CAAAmtForeignFctXY with the given input parameters. It then checks the type of the generated objects. It gets some evaluations and checks that they are correct.

//
// 1-Creation of the function 
//
double a = 1.;
double b = 2.;
double c = 3.;
double d = 10.;

//(u,v) -> F(u,v) = a*u + b*v + c * cos(u)*cos(v) + d
CAAAmtForeignFctXY f(a,b,c,d);

// check the type
if (FALSE== f.IsAKindOf("CAAAmtForeignFctXY") ) return (1);
if (FALSE== f.IsAKindOf("CATMathFunctionXY") )    return (2);

//
// 2-Use the evaluators.
//
double u=0., v=0.;
double val = f.Eval (u,v);
if (val != (c+d))                                 return (3);

// first derivative in u
u = 0.; 
v = CATPIBY4;
val = f.EvalFirstDerivX(u,v);
if (val != (a-c*sin(u)*cos(v)) )                  return (4);

// simultaneous evaluation at a point
double fu, fv, fu2 , fuv , fv2;
f.Eval( u,  v, OptionEvalSecondDeriv, &val, &fu, &fv, &fu2, &fuv, &fv2 );

if (fv2 != (-c*cos(u)*cos(v)) )                   return (5);

The case of the multi evaluation is also addressed as follows: A CATMathIntervalND (N=2) is created, defining the domain of the evaluation. The Eval method is then called, only asking the evaluation of the function and its first derivative. The NULL pointer corresponds to the fact that the second derivatives are not asked.

The values are then compared to those obtained by a direct computation, in order to test the result.

// simultaneous evaluates the tangents at grid points.
// 
double umin       = 0.;
double umax       = CATPIBY4;
double vmin       = 0.;
double vmax       = CATPIBY2;
double aMinMax[4] = {umin, umax, vmin, vmax}; 
CATMathIntervalND domain(2,aMinMax);

long nb[2]    = {10,20};             // number of point in each direction of the grid
long tot      = nb[0]*nb[1];
double * aVal = new double [tot];
double * aFu  = new double [tot];
double * aFv  = new double [tot];
f.Eval(domain, nb, OptionEval+OptionEvalFirstDeriv , aVal, aFu, aFv, NULL, NULL ,NULL);

// checks the evaluation of uij, vij, 0 <= i <= nb[0],  
// 0 <= j <= nb[1]--> aVal[nb[1]*i+j]

int i=2, j=14;
double uij = umin + (umax-umin)*(i)/(nb[0]-1);
double vij = vmin + (vmax-vmin)*(j)/(nb[1]-1);
cout << aVal[nb[1]*i+j] << ", "<< a*uij + b*vij + c*cos(uij)*cos(vij) +d << endl;
if (aVal[nb[1]*i+j] != (a*uij + b*vij + c*cos(uij)*cos(vij) +d) ) return (6);

delete [] aVal;
aVal = NULL;
delete [] aFu;
aFu = NULL;
delete [] aFv;
aFv = NULL;

[Top]

In Short

This use case demonstrates a concrete case of introduction of a new class of foreign functions.

Moreover, it illustrates the use of any mathematical functions.

[Top]

References

[1]	Building and Launching a CAA V5 Use Case
[Top]

History

Version: 1 [Mar 2000]	Document created
[Top]

Geometric Modeler

Mathematics