Creating a Curvature Mapping

This task will show you how to create an editable and associative curvature mapping on any mesh, e.g. to help you select iso-curvature points.

There are five curvatures:

  • Maximum,
  • Minimum,
  • Mean,
  • Gaussian,
  • Absolute.

The geometric construction of the maximum and minimum curvatures is the following:
let be a plane containing the normal to the surface in a given point.
This plane cuts the surface along a curve that has a given curvature in this point.
If this plane rotates around the normal, the curvatures of the curves intersecting
the surface will vary between two utmost values.
These two values are the maximum (KM) and the minimum (Km) curvatures.

The mean curvature is equal to (KM+Km)/2.
The utmost values appear where the surface is the most warped.
The mean curvature is largely used to detect irregularities on the surface.
A minimal surface is characterized by a null mean curvature.

The gaussian curvature is equal to KM.Km.
It describes the local shape of a surface in one point:

  • if it is positive, the point is elliptic,
    i.e. the surface has locally the shape of an ellipsoid around that point,
  • if it is negative, the surface is hyperbolic in this points,
    i.e. the local shape is a horse saddle,
  • it it is null, the surface is parabolic in this point,
    i.e. one of the maximum or minimum curvatures is null in this point.
    The cone and the cylinder are two surfaces where all points are parabolic.

The absolute curvature is equal to |KM|+|Km|.
It is used to detect the surface areas where the surface is locally almost flat
(the absolute curvature is almost null).
Open the SurfNetwork.CATPart from the samples directory. Send all elements but Polygon to the NoShow.

  1. Click Curvature Mapping .
    The Curvature Mapping dialog box is displayed.

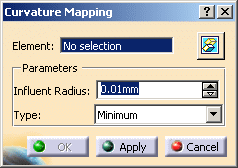
  2. Select Polygon as the Element to process.
    The mesh may not be non-manifold and must contain one single cell.
    Click to hide the input element.

  3. An Influent Radius is proposed.
    By default, it is 1/100 of the diagonal of the bounding box. In this case 2.956mm:

    For each vertex, this radius defines a sphere centered on this vertex.
    All vertices and edges inside this sphere influence the resulting curvature value at this vertex.
    If the Influent Radius is small, the result will be noisy,

    if it is large, the curvature will be smoothed.

  4. Select the type of curvature to apply from the drop-down list:

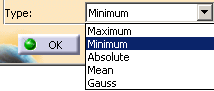
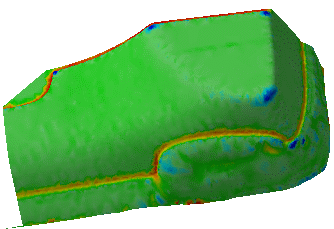
  5. Click Apply. The curvature mapping is displayed:

  6. Click OK to validate and exit the dialog box. A feature Curvature Mapping.x is created in the specification tree. If necessary, double-click its name to edit it.